多元线性回归

一元线性回归

什么是线性

理解：

http://blog.itpub.net/29829936/viewspace-2649379/ 来自 “ ITPUB博客

线性是指 参数是线性关系 ln（xi）只是对 xi 进行了处理不影响什么

当前目标是确定最符合训练数据的参数a和b的值。

这可通过测量每个输入x的实际目标值y和模型f（x）之间的失配来实现，并将失配最小化。这种失配（\= 最小值）被称为误差函数。

有多种误差函数可供选择，但其中最简单的要数RSS（构造出了一个凹函数 好找最小值），即每个数据点x对应的模型f（x）与目标值y的误差平方和。

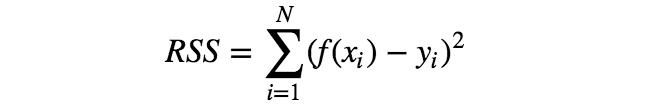
利用误差函数的概念，可将“确定最符合训练数据的参数a、b”改为“确定参数a、b，使误差函数最小化”。

计算一下训练数据的误差函数。

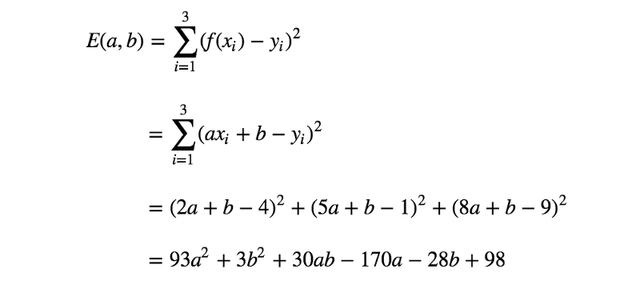
上面的等式就是要求最小值的误差函数。但是，怎样才能找到参数a、b，得到此函数的最小值呢？为启发思维，需要将该函数视觉化。

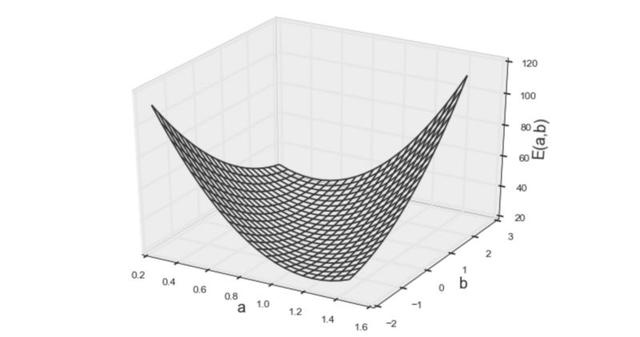
但是无论真么改变函数f（x）都只是改变带入的数据 不影响RSS的形状

内生性

引例

定义

相关就是内生性

危害：不满足回归系数估计的无偏与一致性

误差项

$$\hat\mu_i = y_i-\hat\beta_0-\hat\beta_1x_i$$

假设 真实的为

$$y_i = \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3\\ 是\beta_2x_2+\beta_3x_3 么还应该有\beta_0-\hat\beta_0+(\beta_1-\hat\beta_1)x_1?$$

那误差项就是 所有与y相关 但是没有添加在模型中的（）

如果与已经添加的相关就存在内生性

数学证明

为什么危害（无偏与一致性）

怎么判断内生性

弱化内生性

一、区分变量（？）

原因：解释变量一般很多

变量分为

• 核心解释变量

  我们最感兴趣的变量，因此我们特别希望得到对其系数的 一致估计（当样本容量无限增大时，收敛于待估计参数的真值）

• 控制变量

  我们可能对于这些变量本身并无太大兴趣；而之所以把它们也 放入回归方程，主要是为了“控制住”那些对被解释变量有影响的遗漏因素。

应用：在实际应用中，我们只要保证核心解释变量与𝝁不相关即可。

虚拟变量

用于回归中处理定性变量，例如性别、地域等

解释

多分类

找出一组作为所有的对照 两两比较

可以这样叙述

回归建模步骤

一、描述性统计

指标分类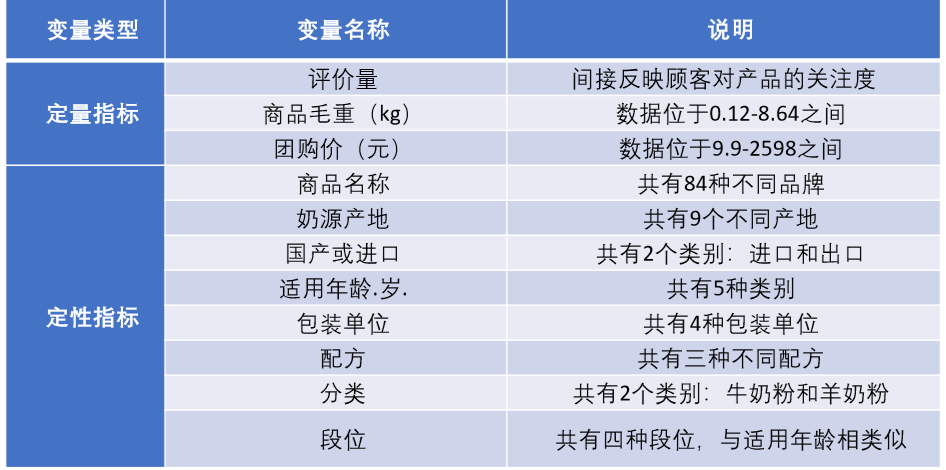

得到表格

• 定量数据

  sum（marize）变量1 变量2… 变量n

• 定性数据

  tab（ulate）变量名，gen（A）

  生成对应的频率分布 并 生成变量A1 A2…An

二、回归

Stata基本OLS

reg（ress）y x1 x2…xn (OLS)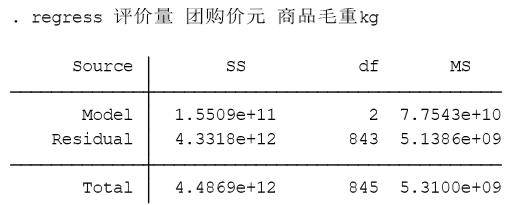

第二列SS对应的是误差平方和，或称变差。
1.第一行为回归平方和或回归变差SSR，表示因变量的预LSSR=测值对其平均值的总偏差。
2.第二行为剩余平方和(也称残差平方和或剩余变差)SSE，是因变量对其预测值的总偏差，这个数值越大，拟合效果越差，y的标准误差即由SSE给出。
3.第三行为总平方和或总变差SST，表示因变量对其平均值的总偏差。

第三列df是自由度(degree of freedom)，第一行是回归自由度dfr，等于变量数目，即dfr=m; 第二为残差自由度dfe， 等于样本数目减去变量数目再减1，即有dfe\=n-m-1;第三行为总自由度dft，等于样本数目减1，即有dft\=n-1。
第四列MS是均方差，误差平方和除以相应的自由度
1.第一行为回归均方差MSR
2.第二行为剩余均方差MSE，数值越小拟合效果越好

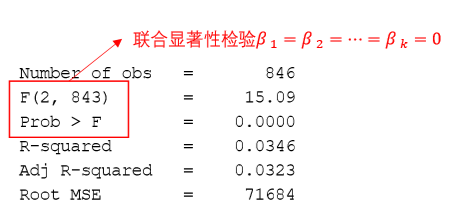
F值，用于线性关系的判定。结合P值对线性关系的显著性进行判断，即弃真概率。所谓“弃真概率”即模型为假的概率，显然1-P便是模型”为真的概率，P值越小越好。对于本例，P=0.0000<0.0001 ,故置信度达到99.99%以上。

---

R- Squared为判定系数(determination coefficignt)，或称拟合优(goodness of fit)，它是相关系数的平方，也是1-SSR/SST，y的总偏差中自变量解释的部分。

(越接近1越好)预测型回归一般才会更看重数值的大小

较小可能是 数据中可能有存在异常值或者数据的分布极度不均匀

---

Adjusted对应的是校正的判定系数

$$R_a^2= 1-\dfrac{SSE/dfe}{SST/dft}$$

我们引入的自变量越多，拟合优度会变大。但我们倾向于使用调整后的拟合优度， 如果新引入的自变量对SSE的减少程度特别少，那么调整后的拟合优度反而会减小

---

Root MSE为标准误差( standard error)，数值越小，拟合的效果越好

$$ROOT\ MSE =\sqrt{MSE}$$

$$Std.\ Err.\ 回归系数的标准误差\\ \sqrt[]{var(\hat\beta_j)} = \sqrt{\dfrac{MSE}{SST_{x_j}(1-R_j^2)}} =\sqrt{\dfrac{MSE*VIF_j}{SST_{x_j}}}\\ R_j^2为x_j对其它自变量进行回归的判决系数即，方差为MSE除以x,中不能被其\\它自变量解释的部分, VIF_j变量x_j的方差扩大因子$$

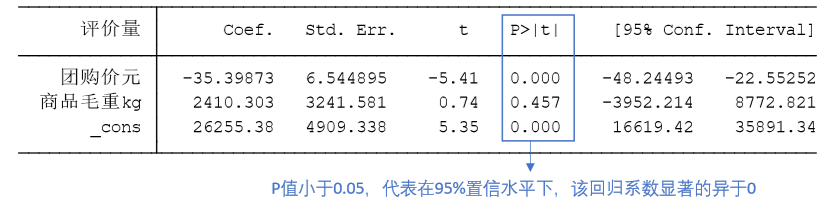
T值\=Coef./Std. Err.

---

P值用于说明回归系数的显著性，一般来说P值<0.1()表示10%显著水平显著，P值<0.05(\*)表示5%显著水平显著，P值 \<0.01(***)表示1%显著水平显著

标准化回归

通过去除量纲的影响来反映自变量之间的重要程度

regress y x1 x2 … xk,beta

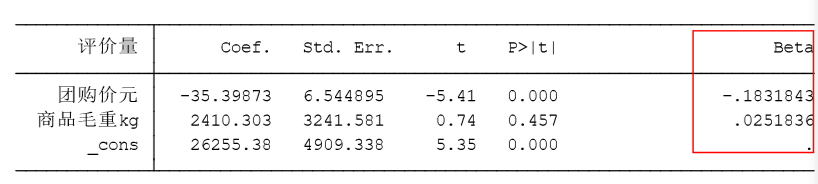
只是多了最后那一列标准化回归系数 对数据进行标准化处理不会影响回归系数的标准误，也不会影响显著性.

三、检验

先进行OLS得到回归结果后 验证扰动项是不是存在异方差，多重共线性

异方差

扰动项存在异方差

（1）OLS估计出来的回归系数是无偏、一致的。

（2）假设检验无法使用（构造的统计量失效了）。

（3）OLS估计量不再是最优线性无偏估计量（BLUE）。

检验

• 画图检验

  • rvfplot (画残差与拟合值的散点图）

  • rvpplotx (画残差与自变量x的散点图)

    画图看出来大致

• BP检验

  estat hettest ,rhs iid

  原假设：扰动项不存在异方差 P值小于0.05，说明在95%的置信水平下拒绝原假设，即我们认为扰动项存在异方差。

• 怀特检验

  estat imtest,white

  怀特检验原假设：不存在异方差

去除异方差的影响

多重共线性

检验

estat vif

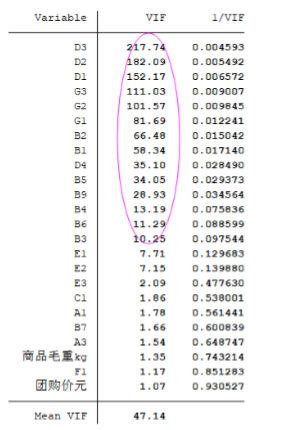
VIF > 10则认为存在严重的多重共线性

四、改进方案

异方差

OLS+稳健的标准误

这是最简单，也是目前通用的方法。只要样本容量较大，即使在异方差的情况下，若使用稳健标准误，则所有参数估计、假设检验均可照常进行。换言之， 只要使用了稳健标准误，就可以与异方差“和平共处”了

regress y x1 x2 … xk,robust

多重共线性

(1)如果不关心具体的回归系数，而只关心整个方程预测被解释变量的能力，则通常可以不必理会多重共线性（假设你的整个方程是显著的）。这是因为多重共线性的主要后果是使得对单个变量的贡献估计不准，但所有变量的整体效应仍可以较准确地估计

(2)如果关心具体的回归系数，但多重共线性并不影响所关心变量的显著性，那 么也可以不必理会。即使在有方差膨胀的情况下，这些系数依然显著;如果没有 多重共线性，则只会更加显著

(3) 如果多重共线性影响到所关心变量的显著性，则需要增大样本容量，剔除导 致严重共线性的变量（不要轻易删除哦，因为可能会有内生性的影响），或对 模型设定进行修改。